Если
два проводника имеют такую форму, что создаваемое ими электрическое
поле сосредоточено в ограниченной области пространства, то образованная
ими система носит название конденсатора, а сами проводники называют
обкладками конденсатора.
Сферический конденсатор. Два проводника, имеющие форму концентрических
сфер с радиусами R1 и R2 (R2
> R1), образуют сферический конденсатор. Используя
теорему Гаусса, легко показать, что электрическое поле существует только
в пространстве между сферами. Напряженность этого поля
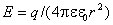 ,
,
где
q - электрический заряд внутренней сферы;
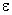
- относительная диэлектрическая проницаемость среды, заполняющей пространство
между обкладками;
r - расстояние от центра сфер, причем
R1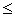
r
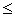 R2
R2.
Разность потенциалов между обкладками
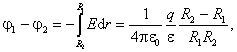
и емкость сферического конденсатора
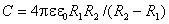 .
.
Цилиндрический конденсатор представляет собой два проводящих коаксиальных
цилиндра радиусами
R1 и
R2 (
R2
>
R1). Пренебрегая краевыми эффектами на торцах цилиндров
и считая, что пространство между обкладками заполнено диэлектрической
средой с относительной проницаемостью
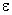
,
напряженность поля внутри конденсатора можно найти по формуле:
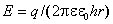 ,
,
где
q - заряд внутреннего цилиндра;
h - высота цилиндров
(обкладок);
r - расстояние от оси цилиндров. Соответственно, разность
потенциалов между обкладками цилиндрического конденсатора и его емкость
есть
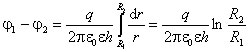
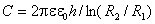
Плоский конденсатор. Две плоские параллельные пластины одинаковой
площади
S, расположенные на расстоянии
d друг от друга,
образуют
плоский конденсатор. Если пространство между пластинами
заполнено средой с относительной диэлектрической проницаемостью
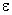
,
то при сообщении им заряда
q напряженность электрического поля
между пластинами равна
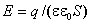
,
разность потенциалов равна
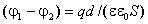
.
Таким образом, емкость плоского конденсатора
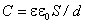
.
Последовательное и параллельное соединение конденсаторов. При
последовательном
соединении n конденсаторов суммарная емкость системы равна
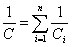
Параллельное соединение n конденсаторов образует систему, электроемкость
которой можно вычислить следующим образом:
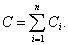
Вопросы
1) Приведите обоснования формул, по которым вычисляется емкость
при последовательном и параллельном соединении конденсаторов
2) Как изменится емкость сферического конденсатора, если внутреннюю сферу
немного сместить от центра

![]() ,
,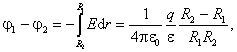
![]() .
.![]() ,
,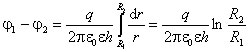
![]()
![]()
![]()