Энергия заряженного проводника. Поверхность проводника является эквипотенциальной. Поэтому потенциалы тех точек, в которых находятся точечные заряды dq, одинаковы и равны потенциалу 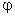проводника. Заряд q, находящийся на проводнике, можно рассматривать как систему точечных зарядов dq. Тогда энергия заряженного проводника

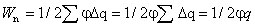
Приняв во внимание определение емкости, можно записать

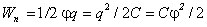
Любое из этих выражений определяет энергию заряженного проводника.

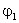
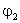
Энергия заряженного конденсатора. Пусть потенциал обкладки конденсатора, на которой находится заряд +q, равен , а потенциал обкладки, на которой находится заряд -q, равен . Энергия такой системы

.

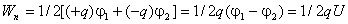Энергию заряженного конденсатора можно представить в виде

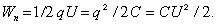
Энергия электрического поля. Энергию заряженного конденсатора можно выразить через величины, характеризующие электрическое поле в зазоре между обкладками. Сделаем это на примере плоского конденсатора. Подстановка выражения для емкости в формулу для энергии конденсатора дает

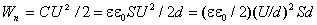
Частное U / d равно напряженности поля в зазоре; произведение S·d представляет собой объем V, занимаемый полем. Следовательно,

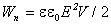
Если поле однородно (что имеет место в плоском конденсаторе при расстоянии d много меньшем, чем линейные размеры обкладок), то заключенная в нем энергия распределяется в пространстве с постоянной плотностью w. Тогда объемная плотность энергии электрического поля равна

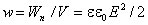
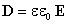
C учетом соотношения можно записать

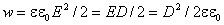
В изотропном диэлектрике направления векторов D и E совпадают и
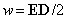
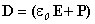
Подставим выражение , получим

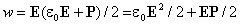
Первое слагаемое в этом выражении совпадает с плотностью энергии поля в вакууме. Второе слагаемое представляет собой энергию, затрачиваемую на поляризацию диэлектрика. Покажем это на примере неполярного диэлектрика. Поляризация неполярного диэлектрика заключается в том, что заряды, входящие в состав молекул, смещаются из своих положений под действием электрического поля Е. В расчете на единицу объема диэлектрика работа, затрачиваемая на смещение зарядов q_i на величину dr_i, составляет

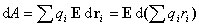
Выражение в скобках есть дипольный момент единицы объема или поляризованность диэлектрика Р. Следовательно, .
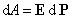
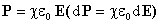
Вектор P связан с вектором E соотношением . Подставив это выражение в формулу для работы, получим

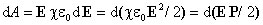
Проведя интегрирование, определим работу, затрачиваемую на поляризацию единицы объема диэлектрика

.

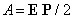Зная плотность энергии поля в каждой точке, можно найти энергию поля, заключенного в любом объеме V. Для этого нужно вычислить интеграл:

---

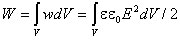
Вопросы

1) Напишите соотношения, выражающие энергию заряженного конденсатора. Опишите ситуации, в которых использование какого-либо из соотношений предпочтительно
2) Напишите соотношения (их 3), выражающие объемную плотность энергии электрического поля. Выразите эти же соотношения через плотность свободных и связанных зарядов.