Немецкий физик Г. Ом экспериментально установил закон, согласно которому сила тока, текущего по однородному (отсутствуют сторонние силы) металлическому проводнику, пропорциональна падению напряжения на проводнике:

.

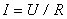Сопротивление проводника. Величина R называется электрическим сопротивлением проводника. Единица сопротивления - 1 Ом. Для однородного цилиндрического проводника

,

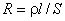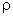
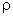
где l - длина проводника; S - площадь его поперечного сечения; - зависящий от свойств материала коэффициент, называемый удельным электрическим сопротивлением. В системе СИ единица измерения есть .

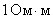
Дифференциальная форма закона Ома. Найдем связь между плотностью тока j и напряженностью поля Е в одной и той же точке проводника. В изотропном проводнике упорядоченное движение носителей тока происходит в направлении вектора Е. Поэтому направления векторов j и Е совпадают.
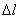
Рассмотрим в однородной изотропной среде элементарный объем с образующими, параллельными вектору Е, длиной , ограниченной двумя эквипотенциальными сечениями 1 и 2 (рис. 4.3).

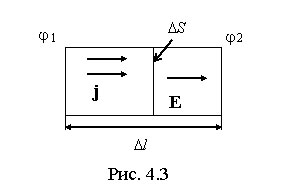
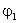
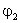
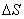
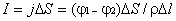
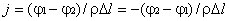
Обозначим их потенциалы и , а среднюю площадь сечения через . Используя закон Ома, получим для тока , или для плотности тока , следовательно

.

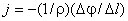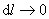
Перейдем к пределу при , тогда рассматриваемый объем можно считать цилиндрическим, а поле внутри него однородным, так что

,

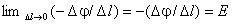где Е - напряженность электрического поля внутри проводника. Учитывая, что j и Е совпадают по направлению, получаем

.

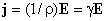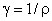
Это соотношение является дифференциальной формой закона Ома для однородного участка цепи. Величина называется удельной проводимостью.

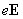
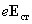
На неоднородном участке цепи на носители тока действуют, кроме электростатических сил , еще и сторонние силы , следовательно, плотность тока в этих участках оказывается пропорциональной сумме напряженностей. Учет этого приводит к дифференциальной форме закон Ома для неоднородного участка цепи.

.

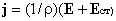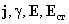
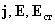
От закона Ома в дифференциальной форме легко перейти к интегральной форме. Рассмотрим неоднородный участок цепи. Внутри этого участка выберем контур тока, удовлетворяющий следующим условиям: в каждом сечении, перпендикулярном к контуру, величины имеют с достаточной точностью одинаковые значения; векторы в каждой точке направлены по касательной к контуру.

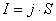
Вследствие закона сохранения заряда сила постоянного тока в каждом сечении должна быть одинаковой. Поэтому величина постоянна вдоль контура. Тогда, заменяя j отношением , получаем

.

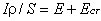Умножим это соотношение на dl и проинтегрируем вдоль контура:

,

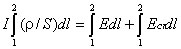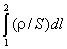
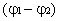
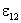
где представляет собой суммарное сопротивление участка цепи, первый интеграл в правой части - разность потенциалов на концах участка, а второй интеграл определяет ЭДС , действующую на участке цепи. Таким образом .

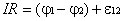
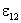
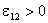
ЭДС , как и сила тока I, величина алгебраическая. В случае, когда ЭДС способствует движению положительных носителей тока в выбранном направлении (в направлении 1-2), . Если ЭДС препятствует движению положительных носителей в данном направлении, то :

.

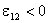
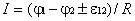Последняя формула выражает закон Ома для неоднородного участка цепи. Для замкнутой цепи закон Ома имеет вид

,

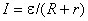где R - сопротивление нагрузки, r - внутреннее сопротивление источника тока.

---

Вопросы

1) Какова связь между проводимостью и сопротивлением, удельной проводимостью и удельным сопротивлением
2) Какой вид имеет вольт-амперная характеристика металлического элемента: линейный или экспоненциальный
3) Каковы правила знаков для силы тока и ЭДС при записи закона Ома для неоднородного участка цепи
4) Поясните когда необходимо использовать закона Ома и интергальной форме, а когда в дифференциальной