Пример 1.
Вычислите заряд Q, протекший по однородному проводнику с сопротивлением R = 3 Ом, если разность потенциалов между концами проводника равномерно увеличивается за время от значения до .

Решение

Разность потенциалов линейно зависит от времени.. Сила тока в проводнике изменяется в соответствии с функцией , поэтому элементарный заряд, протекший по проводнику за время dt, составит . Интегрируя элементарные заряды по времени в пределах от 0 до , получаем

.

Пример 2.
1. Определите плотность электрического тока, если за время через проводник, площадь поперечного сечения которого , прошло .
Ответ: ; .
2. Определите разность потенциалов на реостате, изготовленном из металлического провода ( ) длиной 7,5 м. Плотность тока равна .
Ответ: ; .

Пример 3.
1. Определите скорости дрейфа ионов воздуха на расстоянии от центра металлического шарика , если шарик заряжен до потенциала . Подвижности ионов воздуха и .
Ответ: подвижностью носителя заряда (электрона, протона, иона и др.) называется отношение , поэтому , где , следовательно
2. Определите скорость дрейфа электронов и время их прохождения через пластину кремния толщиной , если к пластине приложена разность потенциалов . Подвижность электронов в кремнии .
Ответ: ; ; ; .

Пример 4.
1. Принимая, что на каждый атом меди приходится один свободный электрон, оцените, сколько времени t потребуется для перемещения свободного электрона по медному проводу длиной l = 15 км и сечением 1 мм² от одного конца провода до другого. По проводу течет ток при разности потенциалов
Ответ: около лет.
2. Используя данные предыдущей задачи, определите результирующую силу F, действующую на все электроны проводимости .

Решение

,

где - плотность меди, - молярная масса меди. Объединяя эти соотношения, получаем .

Пример 5.
1. Металлическому шару (сфере) радиуса R сообщен заряд Q. Шар погружен в однородную среду с удельным сопротивлением и диэлектрической проницаемостью . Определите силу тока I, обусловленного стеканием заряда с шара.

Решение

На расстоянии r > Rот центра шара плотность электрического тока , подставляя выражение для напряженности поля вне шара получим . Сила тока через воображаемую сферическую поверхность радиуса r равна .
2. Пусть все параметры и их обозначения такие же, как в предыдущей задаче, но шар заряжен до потенциала . Какова сила I тока утечки заряда с шара?
Ответ: справедливы все пояснения к предыдущей задаче, заряд на шаре и .
3. Определите, в соответствии с какой функцией изменяется заряд на шаре, помещенном в электропроводящую среду?

Решение

Убывающий заряд есть , но и ток зависит от времени , следовательно или .
Интегрируем это дифференциальное соотношение в пределах справа от 0 до t, слева от Q до . Тогда получаем

,

где - максвелловское время релаксации. В соответствии с такой же функцией изменяется и потенциал шара и сила тока утечки .
4. Зазор между обкладками плоского конденсатора заполнен стеклом ( = 6) с удельным сопротивлением . Электроемкость конденсатора . Определите силу тока утечки конденсатора при разности потенциалов на его обкладках .
Ответ: ; для определения R воспользуйтесь соотношением , тогда ; .

Пример 6.
Длинный проводник круглого сечения радиуса а изготовлен из электропроводящего материала, удельное сопротивление которого изменяется только в зависимости от расстояния r до оси проводника в соответствии с функцией , где - постоянная ( ). Вычислите напряженность ЭСП в проводнике, если по нему течет ток силой I.

Решение

Очевидно, что напряженность ЭСП во всех точках сечения проводника одинакова. Разбиваем мысленно тогда проводник на соосные цилиндрические слои радиусов r и толщиной dr, по каждому из которых течет элементарный ток силой

.

Интегрируем эти элементарные токи по сечению проводника и получаем

, откуда .

Пример 7.
Сферический конденсатор с радиусами и обкладок заполнен однородным диэлектриком с проницаемостью и удельным сопротивлением . Рассчитайте сопротивление конденсатора между обкладками.

Решение

Сила тока утечки между обкладками , где разность потенциалов между обкладками или сила тока . Используя дифференциальную форму закона Ома, имеем . Окончательно, получаем результат

.

Отметим на этом частном примере закономерность, имеющую общий характер для любых конденсаторов: произведение определяется только диэлектрическими и электропроводящими свойствами диэлектрика (величина имеет размерность времени и ее называют максвелловским временем релаксации). Если для конденсатора известен лишь один из параметров R или С, другой может быть непосредственно определен из выражения для .

Пример 8.
1. Пространство между обкладками плоского конденсатора заполнено однородным диэлектриком с и удельным сопротивлением . Электроемкость конденсатора C = 4 нФ. Определите сопротивление R между обкладками конденсатора.

Решение

Из выражения для максвелловского времени релаксации следует, что

; .

Другой подход: сопротивление конденсатора можно определить также как , где отношение следует из выражения для электроемкости плоского конденсатора . Получаем то же выражение для R.
2. Плоский конденсатор (обозначения S и d общепринятые) заполнен целиком диэлектриком, удельное сопротивление которого изменяется только в направлении оси x, перпендикулярной обкладкам, в соответствии с функцией , - постоянная ( ). Начало оси x совмещено с одной из обкладок. Определите сопротивление такого конденсатора.

Решение

Представим диэлектрический слой между обкладками как множество последовательно соединенных плоских конденсаторов толщиной dx, элементарное сопротивление каждого из которых

.

Суммируя сопротивления всех элементарных конденсаторов, получаем результат

.

Пример 9.
Сферический конденсатор с радиусами и внутренней и внешней обкладок заполнен однородным диэлектриком с проницаемостью и удельным сопротивлением . Рассчитайте сопротивление конденсатора.

Решение

Конденсатор можно рассматривать как последовательное соединение множества тонкостенных сферических проводников толщиной dr и радиусом r; сопротивление каждого из них . Суммируя сопротивления всех таких проводников по объему конденсатора (интегрируя по переменной r от до ), получаем

.

Такое же выражение для сопротивления конденсатора было получено в примере 7 с использованием другого подхода.

Пример 10.
Цилиндрический конденсатор длиной l и радиусами и соосных цилиндров заполнен диэлектриком с удельным сопротивлением . Определите сопротивление между обкладками конденсатора.

Решение

Представим мысленно конденсатор как множество соосных цилиндрических конденсаторов длиной l, толщиной dr, площадью обкладок . Элементарное сопротивление каждого такого конденсатора . Поскольку все такие конденсаторы "соединены" последовательно, сопротивление всего конденсатора .

Пример 11.
На концах однородного проводника с сопротивлением в интервале времени с разность потенциалов увеличивается в соответствии с линейной функцией от значения до . Как во времени изменяется количество выделившейся в проводнике энергии ? Определите энергию, выделившуюся в проводнике к моменту времени .

Решение

Разность потенциалов изменяется в соответствии с функцией . Количество энергии, выделившейся в момент времени в пределах от 0 до t в интервале dt есть . Интегрируем эти элементарные энергии по времени в пределах от 0 до и получаем ответ на первый вопрос:

.

В момент времени имеем .

Пример 12.
Сила тока в проводнике с сопротивлением равномерно увеличивается в соответствии с линейной функций от за время . Определите энергию , выделившуюся в проводнике за этот промежуток времени.

Решение

Сила тока в проводнике изменяется в соответствие с функцией , поэтому элементарное количество энергии . Далее интегрируем элементарные энергии по времени в пределах от и получаем

Пример 13.
Конденсатору с электроемкостью C сообщили заряд , а затем в момент времени с замкнули его на резистор с сопротивлением R. Представьте зависимость от времени с количества энергии, выделившейся в резисторе.

Решение

Искомое количество энергии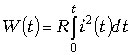 . Временные зависимости заряда, силы тока, разности потенциалов разряжающегося конденсатора обсуждалась ранее, т.е.
, где .
Интегрируем квадрат силы тока и получаем результат

,

где - время релаксации.

Пример 14.
Между обкладками заряженного конденсатора емкостью разность потенциалов . Обкладки конденсатора замыкают резистором с сопротивлением . Сколько энергии W выделится на резисторе через после замыкания обкладок?

Решение

Известно из анализа предыдущих задач, что сила разрядного тока конденсатора , где время релаксации . Элементарная энергия

.

Интегрируем элементарные энергии по времени в пределах 0 - и получаем результат
; .

Пример 15.
Покажите, что распределение сил токов и между двумя резисторами с сопротивлениями R₁ и R₂, соединенными параллельно отвечает минимуму ленц - джоулевой энергии, выделяемой на этом участке цепи.

Решение

В точке разветвления токов . Тепловая мощность выделяемая на участке цепи составит . Эта функция в зависимости от силы тока имеет экстремум: , откуда

.

.Из этих "энергетических" соотношений имеем или .

Пример 16.
В медном проводнике ( , объемом при прохождении постоянного электрического тока за время выделилось энергии. Определите напряженность E электрического поля в проводнике.
Ответ: , следовательно, ; .

Пример 17.
1. Источник с ЭДС и внутренним сопротивлением подключен к нагрузочному резистору с сопротивлением . При каком сопротивлении отдаваемая источником мощность максимальна (режим согласования)? Чему равна максимальная мощность ? Чему равен КПД источника в режиме согласования?

Решение

1) электрическая мощность в нагрузочном резисторе . Исследуем далее эту функцию на экстремум по параметру : , откуда получаем .
2) Максимальная мощность, которую от источника можно передать в нагрузочной резистор, .
3) КПД источника в режиме согласования .

2. При подключении к источнику тока с ЭДС В резистора сопротивлением КПД источника . Какую наибольшую электрическую мощность P_emax можно получить во внешней цепи от такого источника?

Решение

из выражения для КПД определяем внутреннее сопротивление источника . Мощность во внешней цепи максимальна, если обеспечен режим согласования, т. е.
; ; .

3. Потребитель получает от электростанции электрическую мощность . Вычислите сопротивление линии передачи (двух проводов), если потери энергии в проводах составляют от передаваемой энергии. Разность потенциалов на шинах электростанции .

Решение

Отдаваемая электростанцией мощность равна . Мощность потерь в проводах . Составляем соотношение энергетического баланса

.

Из равенства имеем ; .

наверх