
Рассмотрим
произвольный участок цепи постоянного тока, к концам которого приложено
напряжение U. За время t через каждое сечение проводника
проходит заряд ![]() .
Это равносильно тому, что заряд q переносится за время t
из одного конца проводника в другой.
.
Это равносильно тому, что заряд q переносится за время t
из одного конца проводника в другой.
При этом силы электростатического поля и сторонние силы, действующие
на данном участке, совершают работу ![]() .
Разделив работу на время t, за которое она совершается, получим
мощность, развиваемую током на рассматриваемом участке
.
Разделив работу на время t, за которое она совершается, получим
мощность, развиваемую током на рассматриваемом участке ![]() .
.
Эта мощность может расходоваться на совершение работы над внешними телами;
на протекание химических реакций; на нагревание данного участка цепи
и др.
В случае, когда проводник неподвижен и химических превращений в нем
не совершается, работа тока затрачивается на увеличение внутренней энергии
проводника, в результате чего проводник нагревается. Принято говорить,
что при протекании тока в проводнике выделяется тепло
![]() (4.1)
(4.1)
Это соотношение называется законом Джоуля - Ленца. Оно было
экспериментально установлено английским физиком Д. П. Джоулем и подтверждено
точными опытами Э. Х. Ленца.
Если сила тока изменяется со временем, то количество теплоты, выделяющееся
в проводнике за время t, вычисляется по формуле
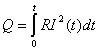 .
.
![]() ,
,
![]() .
.
Вопросы
1) В чем заключается физический смысл удельной тепловой мощности тока2) Напишите закон Джоуля-Ленца в интегральной и дифференциальной формах