Для установления связи между силовой характеристикой электрического поля - напряжённостью и его энергетической характеристикой - потенциалом рассмотрим элементарную работу сил электрического поля на бесконечно малом перемещении точечного заряда q: dA = q E dl, эта же работа равна убыли потенциальной энергии заряда q: dA = - dW_п = - q d, где d - изменение потенциала электрического поля на длине перемещения dl. Приравнивая правые части выражений, получаем: E dl = -d или в декартовой системе координат

E_x dx + E_y dy + E_z dz = -d,      (1.8)

где E_x, E_y, E_z - проекции вектора напряженности на оси системы координат. Поскольку выражение (1.8) представляет собой полный дифференциал, то для проекций вектора напряженности имеем

откуда 

.

Стоящее в скобках выражение является градиентом потенциала j, т. е.

E = - grad = -Ñ.

Напряжённость в какой-либо точке электрического поля равна градиенту потенциала в этой точке, взятому с обратным знаком. Знак «минус» указывает, что напряженность E направлена в сторону убывания потенциала.

Рассмотрим электрическое поле, создаваемое положительным точечным зарядом q (рис. 1.6). Потенциал поля в точке М, положение которой определяется радиус-вектором r, равен = q / 4pe₀er. Направление радиус-вектора r совпадает с направлением вектора напряженности E, а градиент потенциала направлен в противоположную сторону. Проекция градиента на направление радиус-вектора

.

Проекция же градиента потенциала на направление вектора t, перпендикулярного вектору r, равна

,

т. е. в этом направлении потенциал электрического поля является постоянной величиной ( = const).

В рассмотренном случае направление вектора r совпадает с направлением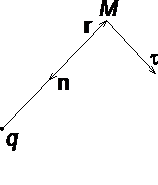
рис. 1.6

силовых линий. Обобщая полученный результат, можно утверждать, что во всех точках кривой, ортогональной к силовым линиям, потенциал электрического поля одинаков. Геометрическим местом точек с одинаковым потенциалом является эквипотенциальная поверхность, ортогональная к силовым линиям.

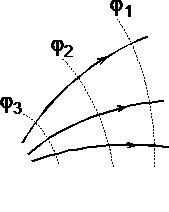
рис. 1.7

При графическом изображении электрических полей часто используют эквипотенциальные поверхности. Обычно эквипотенциали проводят таким образом, чтобы разность потенциалов между любыми двумя эквипотенциальными поверхностями была одинакова. На рис. 1.7 приведена двухмерная картина электрического поля. Силовые линии показаны сплошными линиями, эквипотенциали - штриховыми.

Подобное изображение позволяет сказать, в какую сторону направлен вектор напряжённости электрического поля; где напряжённость больше, где меньше; куда начнёт двигаться электрический заряд, помещённый в ту или иную точку поля. Так как все точки эквипотенциальной поверхности находятся при одинаковом потенциале, то перемещение заряда вдоль нее не требует работы. Это значит, что сила, действующая на заряд, все время перпендикулярна перемещению.

Вопросы

1)    Какова связь между напряженностью и потенциалом. Выведите ее и объясните.

2)    Электростатическое поле имеет вид Е = a i + b j, где a и b константы. Является ли поле однородным. Написать выражение для потенциала поля.

3)    Потенциал некоторого электростатического поля имеет вид = (x² + y² + z²). Что можно сказать о характере поля. Найти модуль напряженности поля в точке с координатами x, y, z

4)   Чему равна работа по перемещению заряда вдоль эквипотенциальной поверхности

наверх