1.9.4. Задачи к параграфам 1.7 - 1.8

Справка.
Отметим, что теорема Гаусса позволяет найти напряженность поля более простыми средствами, чем с использованием формулы для напряженности поля точечного заряда и принципа суперпозиции полей.
Интегральная форма теоремы Гаусса используется при решении прямых задач электростатики: вычисление неизвестной напряженности E и потенциала ЭСП по известному пространственному распределению зарядов.
Ее применение для расчёта электрических полей эффективно в тех случаях, когда поле обладает высокой симметрией, такой, что можно выбрать простую поверхность интегрирования и вычисление потока вектора E свести к умножению модуля напряжённости на площадь поверхности.
Решение обратных задач электростатики, т.е. определение пространственного распределения зарядов по заранее известной структуре ЭСП возможно с использованием дифференциальной формы теоремы Гаусса.
Примеры решения прямых задач, т.е. вычисления напряженности и потенциала ЭСП с использованием теоремы Гаусса предлагаются ниже.

Пример 1. Равномерно заряженная плоскость.
Напряжённость электрического поля, создаваемого бесконечной плоскостью, заряженной с поверхностной плотностью заряда , можно рассчитать, воспользовавшись теоремой Гаусса.

Из условий симметрии следует, что вектор E везде перпендикулярен плоскости. Кроме того, в симметричных относительно плоскости точках вектор E будет одинаков по величине и противоположен по направлению.
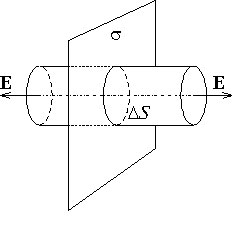
В качестве замкнутой поверхности выберем цилиндр, ось которого перпендикулярна плоскости, а основания расположены симметрично относительно плоскости, как показано на рисунке.
Так как линии напряжённости параллельны образующим боковой поверхности цилиндра, то поток через боковую поверхность равен нулю. Поэтому поток вектора Е через поверхность цилиндра

,

где - площадь основания цилиндра. Цилиндр вырезает из плоскости заряд . Если плоскость находится в однородной изотропной среде с относительной диэлектрической проницаемостью , то

.

Когда напряженность поля не зависит от расстояния между плоскостями, такое поле называют однородным. График зависимости E (x) для плоскости.

Разность потенциалов между двумя точками, находящимися на расстояниях R1 и R2 от заряженной плоскости, равна

Пример 2. Две равномерно заряженные плоскости.
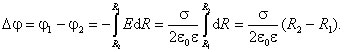
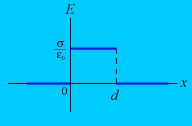
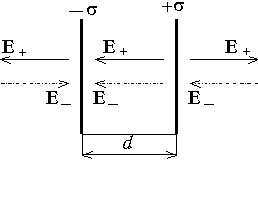
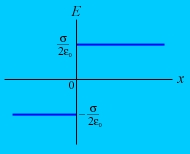
Рассчитаем напряжённость электрического поля, создаваемого двумя бесконечными плоскостями. Электрический заряд распределен равномерно с поверхностной плотностями и . Напряженность поля найдем как суперпозицию напряжённостей полей каждой из плоскостей. Электрическое поле отлично от нуля только в пространстве между плоскостями и равно .

Разность потенциалов между плоскостями , где d - расстояние между плоскостями.
Полученные результаты могут быть использованы для приближённого расчета полей, создаваемых плоскими пластинами конечных размеров, если расстояния между ними много меньше их линейных размеров. Заметные погрешности таких расчётов появляются при рассмотрении полей вблизи краев пластин. График зависимости E (x) для двух плоскостей.


Пример 3. Тонкий заряженный стержень.
Для расчёта напряжённости электрического поля, создаваемого очень длинным заряженным с линейной плотностью заряда стержнем, используем теорему Гаусса.
На достаточно больших расстояниях от концов стержня линии напряжённости электрического поля направлены радиально от оси стержня и лежат в плоскостях, перпендикулярных этой оси. Во всех точках, равноудалённых от оси стержня, численные значения напряжённости одинаковы, если стержень находится в однородной изотропной среде с относительной диэлектрической
проницаемостью .

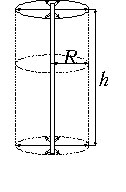
Для расчета напряженности поля в произвольной точке, находящейся на расстоянии r от оси стержня, проведём через эту точку цилиндрическую поверхность
(см. рисунок). Радиус этого цилиндра равен r, а его высота h.
Потоки вектора напряжённости через верхнее и нижнее основания цилиндра будут равны нулю, так как силовые линии не имеют составляющих, нормальных к поверхностям этих оснований. Во всех точках боковой поверхности цилиндра
Е = const.
Следовательно, полный поток вектора E через поверхность цилиндра будет равен

,

По теореме Гаусса, поток вектора E равен алгебраической сумме электрических зарядов, находящихся внутри поверхности (в данном случае цилиндра) делённой на произведение электрической постоянной и относительной диэлектрической проницаемости среды

,

где заряд той части стержня, которая находится внутри цилиндра. Следовательно, напряжённость электрического поля

.

Разность потенциалов электрического поля между двумя точками, находящимися на расстояниях R1 и R2 от оси стержня, найдём, пользуясь связью между напряжённостью и потенциалом электрического поля. Так как напряжённость поля изменяется только в радиальном направлении, то

Пример 4. Заряженная сферическая поверхность.
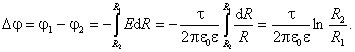
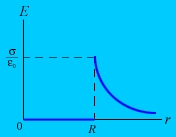
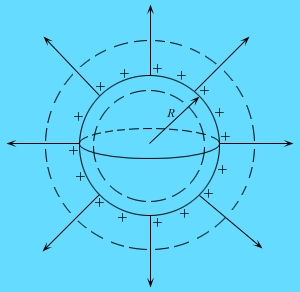
Электрическое поле, создаваемое сферической поверхностью, по которой равномерно распределён электрический заряд с поверхностной плотностью , имеет центрально-симметричный характер.

Линии напряжённости направлены по радиусам от центра сферы, а модуль вектора E зависит только от расстояния r от центра сферы. Для расчёта поля выберем замкнутую сферическую поверхность радиуса r.
При ro<Ro (внутри сферы) Е = 0.
Напряжённость поля равна нулю, так как внутри сферы заряд отсутствует.
При r > R (вне сферы), согласно теореме Гаусса

,

где - относительная диэлектрическая проницаемость среды, окружающей сферу.

.

Напряжённость уменьшается по тому же закону, что и напряженность поля точечного заряда, т. е. по закону .
При ro<Ro (внутри сферы) .
При r > R (вне сферы) .
График зависимости E (r) для сферы.


Пример 5. Заряженный по объему шар из диэлектрика.
Если шар радиусом R из однородного изотропного диэлектрика с относительной проницаемостью равномерно заряжен по объёму с плотностью , то создаваемое им электрическое поле также является центрально-симметричным.
Как и в предыдущем случае, выберем замкнутую поверхность для расчёта потока вектора E в виде концентрической сферы, радиус которой r может изменяться от 0 до .
При r < R поток вектора E через эту поверхность будет определяться зарядом

, так что

При r < R (внутри шара) .
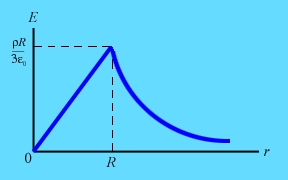
Внутри шара напряжённость возрастает прямо пропорционально расстоянию от центра шара. Вне шара (при r > R) в среде с диэлектрической проницаемостью , поток вектора E через поверхность будет определяться зарядом .
При ro>Ro (вне шара) .
На границе "шар - окружающая среда" напряжённость электрического поля изменяется скачком, величина которого зависит от соотношения диэлектрических проницаемостей шара и среды. График зависимости E (r) для шара ().

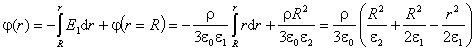Вне шара (r > R) потенциал электрического поля меняется по закону

.

Внутри шара (r < R) потенциал описывается выражением

.

В заключение, приведем выражения для расчета напряженностей полей заряженных тел, различной формы.


наверх
Хостинг от uCoz