|
|
|
|
Взаимодействие точечных зарядов
Пример 1.
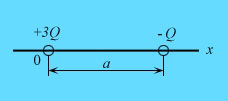
Расстояние между двумя жестко закрепленными точечными зарядами +3Q и - Q равно a = 0,20 м. На каком расстоянии от заряда нужно поместить третий заряд +Q, чтобы он находился в равновесии?
Решение
Свяжем с линией,
соединяющей заряды, ось x, начало O которой совместим с
первым зарядом (см. рисунок). Можно на оси выделить три области 1, 2 и
3.
Из качественных соображений, очевидно, что в областях 1 и 2 равновесие заряда +Q не возможно. Можно надеяться только в области 3 , т.е. при x > a, найти такую точку расположения заряда +Q, в которой равнодействующая всех сил, действующих на этот заряд, будет равняться нулю.
Используя условия равновесия сил, находим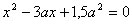 ,
корни которого
,
корни которого
Из качественных соображений, очевидно, что в областях 1 и 2 равновесие заряда +Q не возможно. Можно надеяться только в области 3 , т.е. при x > a, найти такую точку расположения заряда +Q, в которой равнодействующая всех сил, действующих на этот заряд, будет равняться нулю.
Используя условия равновесия сил, находим
![]()
![]()
Из двух значений оправдан только корень со знаком плюс. Следовательно, имеем x1 = 2,36a, так как для него x > a. Таким образом, x1 = 0,472 м или в точке, отстоящей на 0,27 м вправо от второго заряда.
Пример 2.
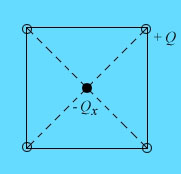
В вершинах квадрата находятся положительные одинаковые заряды Q
по 3,3 10-9 Кл. Какой отрицательный заряд Qx нужно поместить
в центр квадрата для того, чтобы вся система зарядов находилась в равновесии?
Решение
Каждый из зарядов в вершинах квадратов находится в эквивалентных условиях, поэтому достаточно рассмотреть равновесие лишь одного (любого) заряда. Введем как промежуточный параметр сторону квадрата a.На любой из 4-х зарядов со стороны других трех зарядов действуют силы отталкивания, равнодействующая которых направлена по диагонали квадрата в сторону от центра. Значение этой силы
![]()
![]() ; Qx = -3,2 10-9 Кл.
; Qx = -3,2 10-9 Кл.
Пример 3.
Два точечных одинаковых по знаку и модулю заряда Q1 = Q2 = Q жестко закреплены на расстоянии l друг от друга. На линии, соединяющей заряды в точке между зарядами, находится третий точечный заряд q противоположного знака. Материальный носитель этого заряда имеет массу m и имеет возможность без трения двигаться вдоль линии, соединяющей заряды Q1 и Q2 (конструктивно заряд q можно представить как однородно заряженный диэлектрический шар с диаметральным отверстием, через которое проходит прочная диэлектрическая нить, связывающая заряды Q1 и Q2.
Свяжем с линией, соединяющей заряды Q1, Q2 и q ось x; начало оси x совместим с равновесным положением заряда q, т.е. с серединой отрезка l. Покажите, что если вывести заряд q из положения равновесия, т.е. отклонить на расстояние x << l / 2 от положения равновесия и предоставить далее самому себе, он будет совершать гармонические колебания. Какова частота
Решение
При отклонении на x >
0 от положения равновесия заряда q на него будет действовать возвращающая
сила 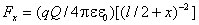
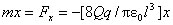 или
или 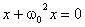
Эти уравнения
суть дифференциального уравнения одномерного классического гармонического
осциллятора. Решение уравнения есть гармоническая функция
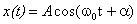 ,
,
где A
и 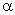 -
постоянные интегрирования (находятся из начальных условий), а
-
постоянные интегрирования (находятся из начальных условий), а 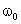 - собственная частота гармонических колебаний;
- собственная частота гармонических колебаний;
![]()
Взаимодействие
точечного заряда с равномерно распределенным
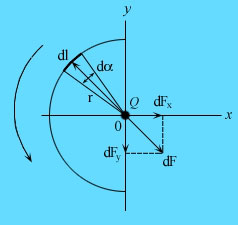
Пример 4.Отрезок тонкой проволоки или диэлектрической нити длиной l сообщен заряд Q и придана форма дуги окружности радиуса R. В центре O этой окружности помещен точечный заряд q. Найдите силу взаимодействия заряженной дуги и точечного заряда q.
Решение
Разбиваем дугу на множество квазиточечных элементов длиной dl, на каждом из которых сосредоточен квазиточечный зарядИз середины произвольного элемента dl в точку O проводим радиус-вектор r (см. рисунок), | r | = R и
![]()
![]()
![]()
![]()
![]()
Тогда имеем при таком соглашении, что
![]()
![]()
Проанализируем частные случаи:
1) Если
2) Если
Пример 5.
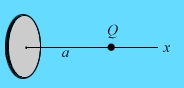
Тонкий жесткий диэлектрический диск радиуса R заряжен равномерно
зарядом Q с поверхностной плотностью ![]() заряда. На оси х диска на расстоянии а от центра диска находится
точечный заряд q. Определите силу взаимодействия этого заряда с
заряженным диском.
заряда. На оси х диска на расстоянии а от центра диска находится
точечный заряд q. Определите силу взаимодействия этого заряда с
заряженным диском.
Решение
Разобьем диск на соосные концентрические
кольца радиусов r < R и шириной dr. Площадь
любого из таких колец равна ![]() ,
поэтому кольцо несет заряд
,
поэтому кольцо несет заряд ![]() .
Элементарная сила взаимодействия заряженного кольца с точечным зарядом
q равна
.
Элементарная сила взаимодействия заряженного кольца с точечным зарядом
q равна
![]()
Далее интегрируем это выражение по r в пределах от 0 до R и получаем ответ
![]()
Проанализируем частные случаи:
1) Пусть а << R, что соответствует представлению диска
как бесконечно протяженной равномерно заряженной тонкой пластины. Тогда,
![]()
2) Если a >> R, то заряженный диск подобен точечному заряду
Пример 6.
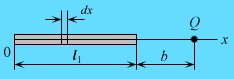
На продолжении тонкого диэлектрического стержня (нити) длиной l1, несущего заряд Q1, равномерно распределенный по длине с линейной плотностью
Решение
Разбиваем стержень на множество
элементов длиной dx каждый. На каждом таком элементе находится
квазиточечный заряд ![]() ,
который действует на заряд Q2 с элементарной силой
,
который действует на заряд Q2 с элементарной силой ![]() .
.
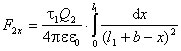
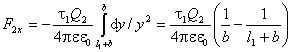
Пример 7.
Плоский конденсатор представляет собою две тонкие протяженные металлические
пластины 1 и 2 расположенные параллельно друг другу. Пластины
заряжены равномерно одинаковыми по модулю, но противоположными по знаку
зарядами с поверхностными плотностями ![]() ,
,
![]() и,
следовательно, притягиваются друг к другу. Определите силу давления p
на пластины.
и,
следовательно, притягиваются друг к другу. Определите силу давления p
на пластины.
Решение
На квазиточечный заряд![]()
Силы давления на обе пластины
одинаковы по модулю, но противоположны по знаку. Для реальных конденсаторов
сила давления может оказаться столь большой, что диэлектрик с проницаемостью
![]() ,
заполняющей пространство между обкладками конденсатора, будет механически
разрушен.
,
заполняющей пространство между обкладками конденсатора, будет механически
разрушен.