|
|
|
|
Справка.
Напряженность - силовой, а значит, векторный параметр электростатического
поля (ЭСП). Если в точку пространства, в котором предполагается существование
ЭСП, помещается пробный заряд qпр (столь малый
по размерам и величине, что своим полем он не искажает изучаемого поля,
и, главное, не меняет распределение зарядов в изучаемой системе) и на
этот заряд со стороны ЭСП действует сила Fпр, то, по
определению, ![]() .
.
Если заряд Q точечный, то из закона Кулона следует, что напряженность
поля ![]() .
Eсли Q > 0, то E одного направления с r; если
Q < 0, то направление E противоположно r.
.
Eсли Q > 0, то E одного направления с r; если
Q < 0, то направление E противоположно r.
Если имеем систему из N точечных зарядов Qi,
то вследствие геометрического сложения сил, действующих на пробный заряд,
сразу приходим к геометрическому принципу суперпозиции для напряжённости
ЭСП: ![]() .
Здесь, Ei - напряжённость ЭСП, создаваемая в
точке зарядом Qi.
.
Здесь, Ei - напряжённость ЭСП, создаваемая в
точке зарядом Qi.
Приведённые соотношения составляют физическую основу одного из методов
расчёта напряжённости ЭСП. Пространственно распределённая система зарядов
разбивается на систему квазиточечных зарядов, для каждого из которых применяется
закон Кулона и, в последующем, принцип суперпозиции.
Этот метод в границах применимости закона Кулона универсален, но иногда
сопряжен с математическими трудностями применения принципа суперпозиции
(на практике с интегрированием). Тогда применяют другие методы.
Пример 1.
Диэлектрический шарик, несущий заряд 4,9 нКл, и имеющий массу 0,4 г, подвешен
в вакууме в поле силы тяжести на жёсткой диэлектрической нити. На какой
угол ![]() отклонится шарик, если его поместить в однородное горизонтальное ЭСП с
напряжённостью 1*105 В/м?
отклонится шарик, если его поместить в однородное горизонтальное ЭСП с
напряжённостью 1*105 В/м?
Решение
В состоянии равновесия равнодействующая всех сил, действующая на шарик,
равна нулю, т. е. ![]() ,
где
,
где ![]() - сила тяжести,
- сила тяжести, ![]() - сила со стороны ЭСП, T - сила натяжения нити. Если изобразить
векторную диаграмму этих сил, то из условия равновесия шарика сразу получим:
- сила со стороны ЭСП, T - сила натяжения нити. Если изобразить
векторную диаграмму этих сил, то из условия равновесия шарика сразу получим:
![]() ;
;
![]() .
.
Пример 2.
Известно, что внутри проводника, при равновесии зарядов на его поверхности,
ЭСП отсутствует. Однако, если проводник движется с ускорением, то в нём
возникает ЭСП. С каким ускорением должен двигаться проводник, чтобы напряжённость
возникшего в нём однородного ЭСП была равна 1 мкВ / м? Какое направление
имеет это ЭСП?
Решение
В неинерциальной системе отсчёта, связанной с ускоренно движущемся проводником,
согласно принципу Д'Аламбера, к реально действующим силам добавляется
сила инерции, равная ma. В такой системе отсчёта перераспределение
свободных электронов закончится, когда результирующая сила, действующая
на электроны, станет равной нулю.
Тогда при условии равновесия электронов получаем ![]() ,
или
,
или ![]() .
Считаем, a
.
Считаем, a![]() 1,5*105
м / с2. Из этих пояснений, очевидно, что сторона проводника,
противоположная направлению вектора а, зарядится отрицательно,
противоположная - положительно. Направление вектора Е возникшего
ЭСП будет антипараллельно вектору а.
1,5*105
м / с2. Из этих пояснений, очевидно, что сторона проводника,
противоположная направлению вектора а, зарядится отрицательно,
противоположная - положительно. Направление вектора Е возникшего
ЭСП будет антипараллельно вектору а.
Пример 3.
Металлический диск радиуса R вращается с угловой скоростью ![]() вокруг оси, перпендикулярной диску и проходящей через его центр. Какая
будет напряженность E(r) ЭСП, возникшего в диске? Как перераспределятся
заряды в диске?
вокруг оси, перпендикулярной диску и проходящей через его центр. Какая
будет напряженность E(r) ЭСП, возникшего в диске? Как перераспределятся
заряды в диске?
Решение
Перераспределение свободных электронов в диске закончится, когда действующие
на них центробежная сила инерции и сила со стороны возникшего ЭСП уравновесятся,
т. е. при условии ![]() ,
откуда
,
откуда ![]() .
.
Поскольку ![]() ,
ясно, что напряжённость возникшего ЭСП будет наибольшей на краю диска
и равной
,
ясно, что напряжённость возникшего ЭСП будет наибольшей на краю диска
и равной ![]() .
Край диска зарядится отрицательно, центральная область - положительно.
.
Край диска зарядится отрицательно, центральная область - положительно.
Пример 4.
Узкий пучок моноэнергетических протонов, скорость которых составляет
V0 = 9,5*104 м / с, влетает в однородное
ЭСП плоского конденсатора параллельно его пластинам. Ось пучка равноудалена
от пластин. При напряжении ![]() на
пластинах конденсатора протоны смещаются от направления первоначального
движения и попадают в точку А экрана.
на
пластинах конденсатора протоны смещаются от направления первоначального
движения и попадают в точку А экрана.
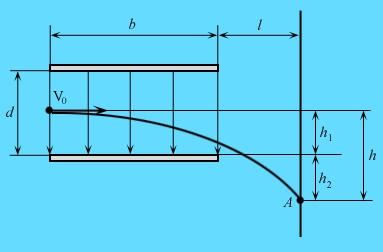
Определите смещение h протонов на экране, если расстояние между
пластинами конденсатора d = 2,4 см, длина пластин b = 6,2
см и расстояние от конденсатора до экрана l = 45 см.
Решение
Принимаем движение протонов в вертикальном и горизонтальном направлениях независимым. При пролёте конденсатора протоны испытывают ускорение в вертикальном направленииЗа пределами конденсатора протоны сместятся ещё по вертикали на расстояние
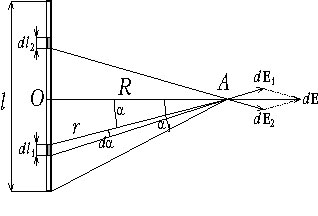
Рассчитайте напряжённость электрического поля, создаваемого тонким заряженным стержнем. Электрический заряд распределяется по длине стержня l равномерно с линейной плотностью
Решение
Определим напряжённость поля в точке А, лежащей на прямой, проходящей через середину стержня О и перпендикулярной к нему (см. рисунок). Точка А находится на расстоянии R от стержня. Выделим на стержне элемент длины dl1, заряд которого ![]()
![]() .
.
Результирующее значение напряжённости поля в точке А находим интегрированием по переменной
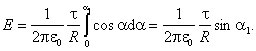
Пример 6.
Тонкое кольцо радиуса R несет заряд Q, равномерно распределенный по кольцу. Определите напряженность ЭСП на оси х кольца на расстоянии а от центра. Ось х перпендикулярна плоскости кольца и проходит через его центр.
Решение
Выделим на кольце элемент длины dl, заряд которого dq. Тогда в точке А, находящейся от элемента dl на расстоянии r, зарядом dq создается поле,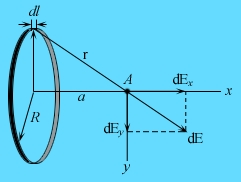
Направлен вектор dE по линии, соединяющей dl с точкой А. Разложим вектор на составляющие:
Второе слагаемое в силу симметрии рассматриваемой фигуры равно 0. Поскольку
Следовательно,
Далее интегрируем, учитывая, что
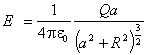 .
.
Пример 7.
Тонкий диэлектрический диск радиуса R заряжен равномерно с поверхностной плотностью
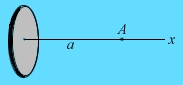
Решение
Разобьем диск на соосные кольцевые зоны радиусов r и толщиной dr На каждом таком выделенном кольце будет заряд![]() .
.
![]() .
.
Обсудим следующие важные частные случаи:
1) пусть ![]() ,
т. е. точка расположена столь близко к диску, что диск представляется
бесконечно заряженной плоскостью. Тогда из сразу получаем
,
т. е. точка расположена столь близко к диску, что диск представляется
бесконечно заряженной плоскостью. Тогда из сразу получаем ![]() .
.
2) Если ![]() ,
то, используя формулы приближённых вычислений, получаем
,
то, используя формулы приближённых вычислений, получаем ![]() ,
где
,
где![]() - заряд на диске.
- заряд на диске.
Этот результат вполне очевиден, ибо в рассматриваемом приближении заряд
на диске представляется точечным.
Пример 8.
Тонкостенный цилиндр радиусом R и длиной l заряжен равномерно
с поверхностной плотностью ![]() заряда. Определите напряжённость ЭСП на оси x цилиндра в точке
А на расстоянии а от одного из его оснований, например, правого,
как показано на рисунке.
заряда. Определите напряжённость ЭСП на оси x цилиндра в точке
А на расстоянии а от одного из его оснований, например, правого,
как показано на рисунке.
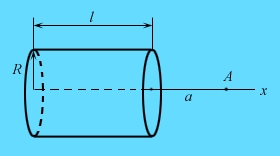
Решение
Разбиваем мысленно цилиндр на кольцеобразные зоны толщиной dx, несущие зарядыКаждая такая зона создаёт в точке А ЭСП с напряжённостью
![]() .
.