1.9.4. Задачи к параграфам 1.7 - 1.8
Справка.
Оба параметра ЭСП, силовой Е и энергетический , тесно взаимосвязаны:

.

Это соотношение иллюстрирует следующую важную особенность ЭСП (как и всякого другого потенциального поля): для полного задания поля нет необходимости сразу задавать оба параметра. Вся информация об одном из параметров содержится и легко может быть восстановлена из информации о первом параметре, что важно при решении практических задач.
Если умножить приведенное соотношение на значение Q точечного заряда, то придем к другому по внешнему виду соотношению:

,

где - потенциальная энергия заряда Q в ЭСП. Это соотношение позволяет решать многие силовые задачи электростатики.
Чтобы использовать первое из соотношений справки для расчета потенциала в соответствии, например, с соотношением , необходимо сделать выбор точки нулевого потенциала:
1. если заряженное тело конечно во всех измерениях, за точку нулевого потенциала принимается очень удаленная от тела точка;
2. если тело протяженно хотя бы в одном измерении (нить, пластина, и др.), то за точку нулевого потенциала принимается какая-либо конечная точка, но этот факт перед решением задачи обязательно оговаривается (см. задачи ниже).

Пример 1.
Найдите коэффициент разложения напряженности ЭСП как градиент потенциала на оси х, перпендикулярной к линии, соединяющей два протона. Расстояние между протонами равно 2а и ось х проходит посередине между протонами. Второе, определите силу действующую на второй протон со стороны ЭСП, создаваемого первым протоном.

Решение

,
.

Потенциальная энергия взаимодействия протонов , поэтому

.

Это, по сути, закон Кулона, в котором вместо r2 появилось, как и должно быть, 4а2.

Пример 2.
Определите напряженность Е ЭСП, потенциал которого зависит только от координат x и y в соответствие с функциями: а) ; б) , где A в обеих формулах константа.
Ответ: а) E = -2A (ix - jy); б) E = -A (iy + jx).

Пример 3.
Определите напряженность Е ЭСП, потенциал которого описывается функцией , где А - постоянный вектор; - радиус-вектор, проведенный из начала декартовой системы координат в точку поля.

Решение

. Тогда .
Поле напряженности ЭСП здесь однородное.

Пример 4.
Пусть потенциал ЭСП в некоторой части пространства описывается функцией , где А и В - постоянные. Определите распределение объемной плотности заряда.

Решение

В соответствие с уравнением Пуассона , где -дифференциальный оператор Лапласа. Данная задача одномерная, поэтому уравнение Пуассона имеет вид , откуда сразу следует ответ:

.

Пример 5.
Пусть потенциал ЭСП внутри заряженного диэлектрического шара изменяется только в зависимости от расстояния r от центра шара в соответствие с функцией , где А и В - постоянные. Определите радиальную зависимость объемной плотности заряда.
Ответ: .

Пример 6.
Используя известное соотношение взаимосвязи между напряженностью и потенциалом ЭСП и предполагая, что структура напряженности ЭСП заряженного кольца радиуса R на оси х кольца известна, определите потенциал на расстоянии а от центра кольца.

Решение

Имеем 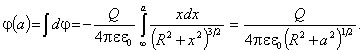. Интегрируем это дифференциальное соотношение по переменной х от бесконечности (где, по соглашению, потенциал заряженного тела с конечными размерами принимается за нуль) до точки с координатой а:

Если а >> R, то - как для точечного заряда.
В центре кольца, т. е. при а = 0, потенциал .
Полезно здесь заметить, что в центре кольца напряженность ЭСП равна нулю.

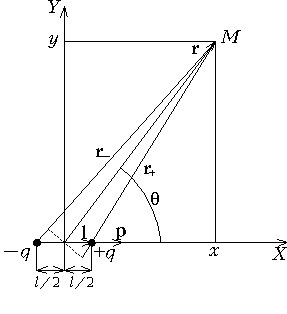
Пример 7.
Получите выражения для напряженности поля и потенциала системы электрических зарядов называемой электрическим диполем.

Решение

Электрическим диполем называют два равных по величине и противоположных по знаку точечных заряда. Расстояние l между зарядами мало по сравнению с расстояниями до рассматриваемых точек поля.
Электрический диполь принято характеризовать двумя параметрами плечом диполя l и электрическим моментом диполя pe. Плечо диполя это вектор, направленный по оси диполя от отрицательного заряда к положительному. Плечо диполя численно равно расстоянию между зарядами. Электрический момент диполя равен произведению величины положительного заряда диполя на его плечо .
Расчет поля диполя проведем для произвольной точки М. Тогда в точке М электрический диполь создаёт поле, потенциал которого


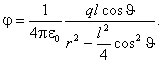
где r+ и r- соответственно расстояния от положительного и отрицательного зарядов диполя до точки М. Они равны

где r - расстояние от середины плеча диполя до точки М; - угол между направлением r и осью x. Тогда выражение для потенциала можно переписать в виде

Учитывая, что r>>l, а , последнее выражение можно упростить:

Для определения напряжённости электрического поля, создаваемого диполем в точке М, воспользуемся связью между потенциалом и напряжённостью электрического поля. Учитывая, что

,

перепишем выражение для потенциала следующим образом:

.

Определим проекции напряжённости поля на координатные оси x и y:

;
.

Модуль вектора напряжённости электрического поля диполя в произвольно выбранной точке М, равен

наверх
Хостинг от uCoz