1.9.3. Задачи к параграфам 1.5 - 1.6
Справка.
Потенциал - это энергетическая, следовательно, скалярная, характеристика ЭСП. Если в некоторой точке пространства, в котором определено ЭСП, известна потенциальная энергия Wpпр пробного заряда qпр, то потенциал ЭСП в этой точке .
Пусть заряд Q, создающий ЭСП, точечный. Пробный заряд qпр при большом удалении (в математическом смысле бесконечно большом) от заряда Q с ним практически не взаимодействует, поэтому их взаимную потенциальную энергию можно принять равной нулю.
При сближении зарядов до конечного расстояния r между ними работа сил ЭСП может быть совершена за счет убыли их энергии взаимодействия, или

,

откуда потенциал точечного заряда .
Потенциал - алгебраическая величина; его знак определяется только знаком заряда Q, создающего ЭСП. Потенциал системы точечных (квазиточечных) зарядов Qi, каждый из которых создает в точке пространства потенциал , составит

.

Это, по сути, выражение принципа суперпозиции для потенциала: потенциал системы зарядов равен алгебраической сумме потенциалов, создаваемых в точке каждым зарядом системы по отдельности.
Эти сведения справки позволяют обосновать весьма важный и универсальный подход к расчету параметров ЭСП реальных макроскопических заряженных тел. Такое тело разбивается на квазиточечные заряды dQi; потенциал поля, создаваемого каждым зарядом находится по известной формуле; далее используется принцип суперпозиции для потенциала. В задачах процедуру алгебраического суммирования заменяют операцией интегрирования по объему заряженного макроскопического тела.
Если точечный заряд Q силами ЭСП перемещается из точки 1 пространства в точку 2, то макроскопическая работа сил ЭСП по перемещению этого заряда в замкнутой системе может быть совершена только за счет уменьшения потенциальной энергии заряда Q в этом ЭСП:

,

где есть разность потенциалов. .

Пример 1.
Тонкое кольцо радиуса R несет заряд Q, равномерно распределенный по кольцу с линейной плотностью заряда. Определите потенциал ЭСП на оси х кольца на расстоянии а от кольца. Ось х перпендикулярна плоскости кольца и проходит через его центр.

Решение

Разбиваем распределенный заряд Q на кольце на квазиточечные заряды , где - элементарная длина кольца.
Тогда элементарный вклад в потенциал точки на оси кольца равен

.

Суммарный потенциал от всех квазиточечных зарядов составит
, где
Заметим на этом частном примере, что знак потенциала определяется только знаком заряда Q, который является источником ЭСП.

Пример 2.
В условии предыдущей задачи предположим, что силами ЭСП точечный заряд q = 10 мкКл перемещается по произвольному пути из центра кольца в точку А. Точка А расположена на оси кольца, на расстоянии а от центра кольца. Вычислите работу сил ЭСП при таком перемещении и разность потенциалов.

Решение

;
.

Пример 3.
В центре плоского кольца радиуса R, несущего равномерно распределенный заряд +Q, расположен отрицательный точечный заряд -Q. Определите напряженность и потенциал ЭСП такой системы зарядов в точке на оси х кольца на расстоянии а от плоскости кольца.

Решение

Используем здесь, принцип суперпозиции для напряженности и потенциала ЭСП системы зарядов (заряженного кольца и точечного заряда). Структура ЭСП заряженного кольца исследована ранее в примерах (1G3, пример 6).

;
;

Если а >> R, то .

Пример 4.
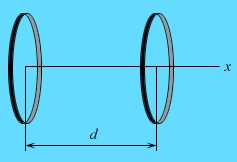
Два тонких проволочных кольца одинаковых радиусов R = 30 см расположены соосно на расстоянии d = 52 см друг от друга (рис.). Кольцам сообщены заряды +Q и - Q = 0,40 мкКл. Определите разность потенциалов между центрами колец.

Решение

Используя результаты решения предыдущих задач, имеем

;
.

Разность потенциалов ; .

Пример 5.
Тонкий диск радиуса R заряжен равномерно по поверхности плотностью заряда . Определите потенциал ЭСП диска в точке А на оси х, проходящей через центр диска перпендикулярно его плоскости, на расстоянии а от центра.

Решение

Разбиваем мысленно диск на концентрические кольцеобразные зоны радиусов r и толщиной dr, несущих элементарные заряды .
На оси каждой такой зоны элементарный потенциал в соответствии с решением предыдущей задачи (пример 1) равен

.

Интегрируя по переменной r в пределах от 0 до R, получаем ответ

.

В центре диска, т. е. при а = 0, потенциал .

Пример 6.
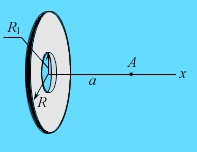
В центре плоского тонкого диска радиуса R2 имеется круглое отверстие радиуса R1. Оставшаяся часть диска заряжена равномерно по поверхности с поверхностной плотностью заряда. Определите напряженность и потенциал ЭСП диска с отверстием в любой точке А на оси диска на расстоянии а от его поверхности.

Решение

Диск с отверстием можно представить как сплошной диск радиуса R2, заряженный с поверхностной плотностью заряда , и наложенным на него другим диском радиуса R1, заряженным зарядом с плотностью . Структура параметров ЭСП заряженного диска известна из рассмотрения предыдущих задач. Используя принцип суперпозиции, получаем:

;
.

Частные случаи: если R1 = 0 (отверстия нет), то

;
.

При R1 = R2 (диска нет) .

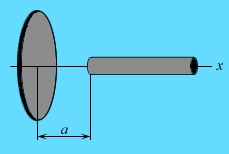
Пример 7.
На оси x тонкого диэлектрического диска радиуса R, заряженного равномерно с поверхностной плотностью заряда , расположен жесткий тонкий стержень длиной l, заряженный с линейной плотностью заряда. Левый конец стержня находится на расстоянии a от центра О диска. Определить:
1) силу взаимодействия стержня и диска;
2) потенциальную энергию стержня в ЭСП диска.

Решение

1) Силовую часть задачи будем решать следующим методом. Разобьем стержень на квазиточечные заряды , на каждый из которых со стороны ЭСП диска действует элементарная сила

.

Интегрируем элементарные силы по длине стержня в пределах от а до (a + l)

.

2) Потенциальную энергию dW квазиточечного заряда dQ на стержне в ЭСП диска найдем как , где - потенциал на оси заряженного диска на расстоянии x от центра (смотри пример выше). Тогда

.

Интегрируем, как и ранее, это выражение в тех же пределах и получаем

.

Подставьте самостоятельно в это выражение пределы интегрирования и скомпонуйте к удобному для вас виду окончательный результат. Поучителен, например, случай a>> l.

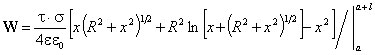Пример 8.
В некоторой точке напряженность ЭСП двукратно ионизованного неподвижного атома гелия ( -частицы) равна . Протон, летящий к частице, имеет скорость . На какое расстояние r0 протон может приблизиться к -частице?

Решение

Система -частица плюс протон является замкнутой и в ней действуют только консервативные силы (здесь кулоновские), поэтому полная энергия системы сохраняется. Следовательно, составляем соотношение энергетического баланса:

.

Подставляя в приведенное соотношение выражение для потенциала

, получаем
.

Откуда следует ; r0 4,9*10-9 м.

наверх
Хостинг от uCoz