Используя выведенные нами дифференциальные соотношения, описывающие свойства электростатического поля и ,

сформулируем уравнение, которое находит применение во многих разделах физики. Поскольку градиент функции представляет собой векторную функцию, то к нему можно применить операцию дивергенции:

div E = - div grad ,

в декартовых координатах

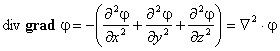
где Ѳ- оператор Лапласа, являющийся суммой вторых производных по координатам. Так что с учетом теоремы Гаусса

.

Это и есть уравнение Пуассона. Уравнение Пуассона является дифференциальным эквивалентом интегрального соотношения, по которому вычисляется потенциал. В тех областях пространства, где заряды отсутствуют (или r = 0), оно превращается в уравнение

,

называемое уравнением Лапласа. В большинстве случаев классическая теория поля занимается исследованием решений этого уравнения. Функции, удовлетворяющие уравнению Лапласа, относятся к классу гармонических функций.

Вопросы

1)    Потенциал в некоторой области определяется формулой
. Найдите плотность зарядов r(x), создающих это поле